隐马尔可夫模型 Hidden Markov Model
隐马尔可夫模型的定义与三个问题,对应三个解决方法
Definetion
对于一个HMM,假设Q是所有可能的隐藏状态的集合,V是所有可能观测状态的集合及
\[Q=\{ q_1,q_2,...,q_N \} \ \ \ \ V=\{v_1,v_2,...,v_M\}\]其中N是所有的隐藏状态数,M是所有观测状态数量。
对于一个长度为T的序列,$I$对应其状态序列,$O$对应其观测序列
\[I=\{i_1,i_2,...i_t\} \ \ \ \ \ O=\{o_1,o_2,...o_t\}\]其中对于任意一个隐藏状态 \(i_t \in Q\),以及任意一个观测状态 \(o_t \in O\)
HMM做了如下两个重要假设
- 齐次马尔可夫链假设,任意时刻的隐藏状态只依赖于它的前一个状态
这种极端的假设是便于求解,如果在时刻t的隐藏状态\(i_t=q_i\),在时刻t+1的隐藏状态\(i_{t+1}=q_j\),则从时刻t到时刻t+1的HMM转移概率\(\alpha_{ij}\)
\[\alpha_{ij}=P(i_{t+1}=q_j| i_{t}=q_i)\]所有情况的状态转移可以用一个N*N的矩阵A来表示,N为所有隐藏状态数
\[A=[\alpha_{ij}]_{N*N}\]-
观测独立性假设,任意时刻的观测状态仅仅只依赖当前时刻的隐藏状态,如果在时刻t的隐藏状态\(i_t=q_i\),时刻t的观测状态\(o_t=v_k\),则从隐藏状态\(q_i\),产生观测状态\(v_k\)的概率为\(b_i(k)\)
\[b_i(k)=P(o_t=v_k|i_t=q_i)\]
从所有隐藏状态转移到观测状态的生成概率可以组成一个N*M矩阵B,N为所有隐藏状态数,M为所有观测状态数
\[B=[b_i(k)]_{N*M}\]另外还有一个初始状态分布 向量\(\pi\)
\[\pi_i=P(i_1=q_i),i=1,2,3,..N\]隐马尔可夫模型由初始状态分布向量\(\pi\),状态转移概率矩阵\(A_{N*N}\)和观测概率生成矩阵\(B_{N*M}\)组成。符号表示为一个三元组
\[\lambda=(\Pi,A,B)\]\(\Pi\ A\ B\) 称为隐马尔可夫模型三要素
Example
网上博客上有很多种例子,这里我选择了知乎高赞中天气的例子作为隐藏状态,我觉得这种场景更符合“隐藏状态”和“观测状态”的字面含义。
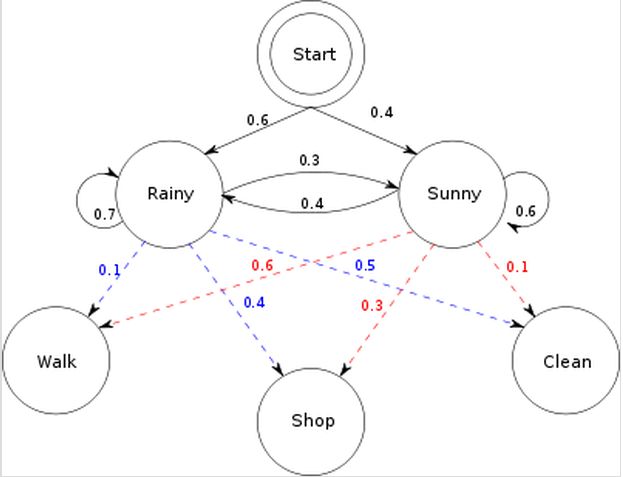
首先上图表现了由三种天气 Sunny , Rainy 下雨,同时上面各个状态之间的状态转移矩阵 [Sunny,Rainy]
\(A=\left [ \begin{matrix} 0.6 & 0.4 \\ 0.3 & 0.7 \\ \end{matrix} \right ]\) 初始状态分布矩阵 \(\Pi=[0.4,0.6]\) 观测产生矩阵 [Walk, Shop, Clean] \(B=\left[ \begin{matrix} 0.6 & 0.3 & 0.1\\ 0.1 & 0.4 & 0.5 \end{matrix} \right ]\) 现在我们要说明什么是 HMM。既是隐形,说明这些状态是观测不到的,相应的,我们可以通过其他方式来『猜测』或是『推断』这些状态,这也是 HMM 需要解决的问题之一。
例子转自链接
举个例子,我女朋友现在在北京工作,而我还在法国读书。每天下班之后,她会根据天气情况有相应的活动:或是去商场购物,或是去公园散步,或是回家收拾房间。我们有时候会通电话,她会告诉我她这几天做了什么,而闲着没事的我呢,则要通过她的行为猜测这几天对应的天气最有可能是什么样子的。
这里天气状态就是隐藏状态序列,而女友的活动就是观测序列。
Three Question
-
评估观测序列概率,即给定模型 \(\lambda=(A,B,\Pi)\) 和观测序列 \(O=\{o_1,o_2,..o_t\}\),计算在模型下观测序列出现的概率 $$P(O \lambda)$$ - 预测问题,也称为解码问题。即给定模型 \(\lambda=(A,B,\Pi)\) 和观测序列 \(O=\{o_1,o_2,..o_t\}\),求给定观测序列条件下,最有可能出现的对应的隐藏状态序列。
-
模型参数学习问题(建模)。即给定多组观测序列\({O_1,O_2,...O_n}\),其中\(O_i=\{o_{i1},o_{i2},...,o_{iT} \}\),估计模型参数 \(\lambda=(A,B,\Pi)\)的参数,该模型下观测序列的条件概率$$P(O \lambda)$$最大
用上面的例子来说明就是:
- 已知整个模型,我女朋友告诉我,连续三天,她下班后做的事情分别是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
- 同样知晓这个模型,同样是这三件事,我女朋友要我猜,这三天她下班后北京的天气是怎么样的。这三天怎么样的天气才最有可能让她做这样的事情。
- 最复杂的,我女朋友只告诉我这三天她分别做了这三件事,而其他什么信息我都没有。她要我建立一个模型,晴雨转换概率,第一天天气情况的概率分布,根据天气情况她选择做某事的概率分布。(惨绝人寰)
问题1,解决方法:Forward Algorithm 前向算法 或者Backward Algorithm 后向算法
问题2,Viterbi Algo 维特比算法
问题3,Baum-Welch Alorithm 鲍姆-韦尔奇算法
其中将详细介绍 1和2,通常这也是在Machine Learning中比较常用的问题解决方案,因为在Training过程中,隐藏序列和观测序列都会同时得到。3的解决方法很复杂,还未看明白。