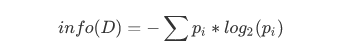决策树 (Decision Tree)__ID3决策树
Auther:Zreal
感谢:
https://blog.csdn.net/lemon_tree12138/article/details/51837983
https://blog.csdn.net/u010089444/article/details/53241218
决策树事例
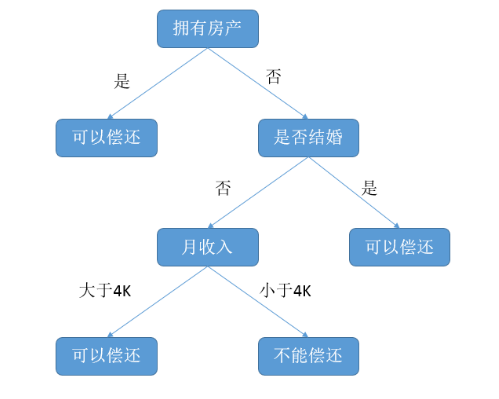
如图所示,机器学习中的决策树是一个预测模型,他表示对象属性和对象值之间的一种映射关旭,书中的每一个节点标示对象属性的判断条件,其分支表示符合节点条件的对象.树的叶子节点表示对象所属的预测结果.
决策树的建立之前
看到上面的决策树的例子,你是否有一个疑问QAQ,为什么在第一层判断的时候判断的是是否拥有房产,然后第二层再判断是否结婚.为什么不能是在第一次判断时,我们就判断是否结婚,第二层判断再判断是否拥有房产(理论上这种也是可行的,但不科学).决策树这样建立的依据是什么?是什么呢?
首先要引入两个概念:
信息熵
直接上公式:
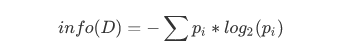
其中pi代表在类别i样本数量占所有样本的比例
可以勉强理解信息熵表示的是一种不确定度.
信息增益
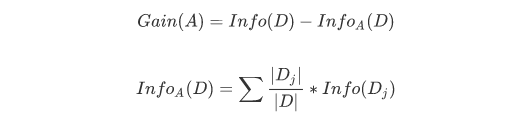
首先解释info_A 表示在选择A特征作为决策树判断节点时,在特征A作用后的整个数据集的信息熵
其中样本D依据选择特征A被分为了若干个子样本Di,对于每个Di求信息熵,然后再求得他们的期望,就代表选择特征A作用后,数据集的信息熵.
信息增益度Gain
从逻辑上来说表示的是数据集D在特征A的作用后,其信息熵减少的值
ID3决策树建立
不涉及官方用语,当你拿到下面的数据集,你该如何建立决策数?
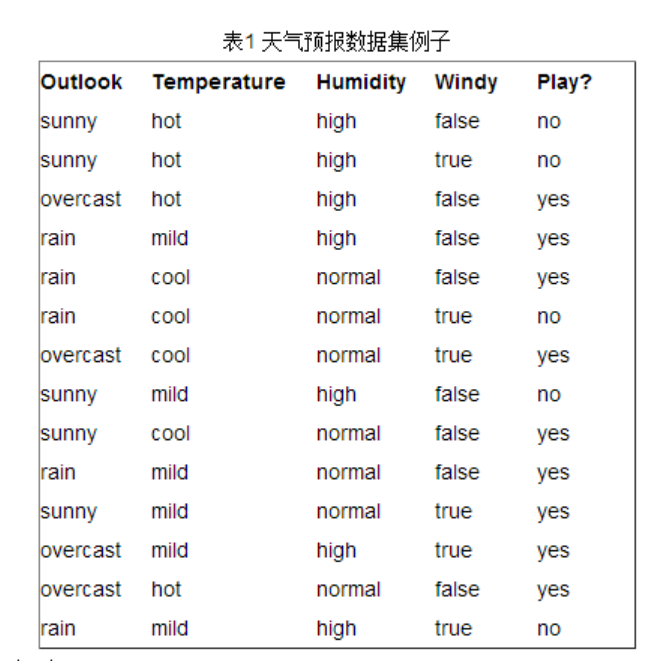
我们可以看到整数据集有四个特征分别是 Outlook,Temperature,Humidity,Windy四个特征,当拿到一条数据,我们要根据这四个特征预测是否可以Play.
如何去选择我们要现在要分类的特征:
遍历所有的特征,算出对应的信息增益,信息增益最大的对应的特征就是决策树此时分类的节点
(可以这样认为,在所有特征中,我们选取可以讲训练集的不决定度(信息熵)降到最小的特征进行分类)
EXAMPLE:
首先定义一个特征集合F={”Outlook”,”Temperature”,”Humidity”,”Windy”}
定义一个初始数据集D如上.
首先我们算出整个数据集的信息熵
\(Info(D)=-\frac{5}{14}*log_2(\frac{5}{14})-\frac{9}{14}*log_2(\frac{9}{14})\)
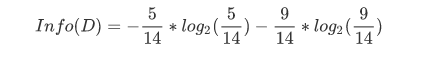
这里我们算Outlook信息增益度:
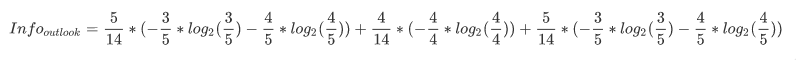
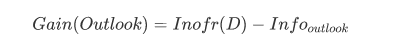
然后依次计算出剩余三个,去除Gain最高的那个特征作为分类特征.
这样就构建了第一层的决策树判断节点,在F中去掉该特征,整个数据集D被特征F划分为若干个Di
(例如如果用outlook作为分类,下面的三个子集分别是):
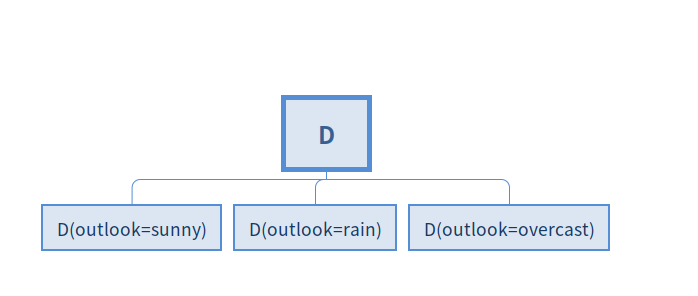
接下来再对每个子数据集进行上述操作即可.
那么问题来了,什么时候递归结束
递归结束的条件:
-
当特征集合F中没有了元素(很容易理解,没有特征可以划分了呗)
-
当该节点下的子集中的元素具有相同的目标属性值(例如在上例中,集合中的所有的play都为yes或no,此时停止递归)
依据信息增益的公式,当所有元素具有相同的目标属性值时,信息增益度为0,就表示即使你选择了特征,也对整个数据集的不决定度没有减小,就可以不选了呀
ID3决策树算法步骤
流程图如下:
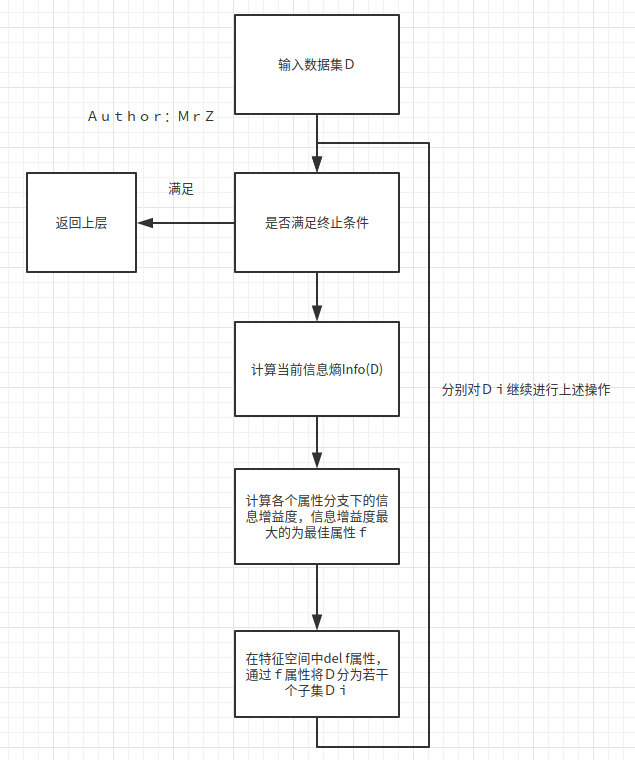
顺便一说:
有这样一个问题,为什么可以用信息熵来衡量这个数据集的不确定度,为什么信息熵要这样计算,恩,我刚开始也有这样的疑问,这到底是为什么呢?
下面的解释大量引用:https://zhuanlan.zhihu.com/p/26486223
十分感谢该博主的解释 很容易理解
信息量
信息量是对信息的度量,就跟时间的度量是秒一样,当我们考虑一个离散的随机变量x的时候,当我们观察到的这个变量的一个具体值的时候,我们接收到了多少信息呢?
多少信息用信息量来衡量,我们接受到的信息量跟具体发生的事件有关。
信息的大小跟随机事件的概率有关。
注意下面两个例子是关键
越小概率的事情发生了产生的信息量越大:湖南产生的地震了
越大概率的事情发生了产生的信息量越小,如太阳从东边升起来了
(是不是很玄学,但是确实很有道理)
一个具体事件的信息量应该是随着其发生概率而递减的,且不能为负。
那么问题又来了,这种减函数这么多为什么要用下面的log公式呢?
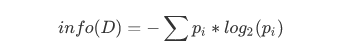
如果我们有俩个不相关的事件x和y,那么我们观察到的俩个事件同时发生时获得的信息应该等于观察到的事件各自发生时获得的信息之和,即:
h(x,y) = h(x) + h(y)
由于x,y是俩个不相关的事件,那么满足p(x,y) = p(x)*p(y).
根据上面推导,我们很容易看出h(x)一定与p(x)的对数有关(因为只有对数形式的真数相乘之后,能够对应对数的相加形式,可以试试)。因此我们有信息量公式如下:
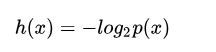
下面解决俩个疑问?
(1)为什么有一个负号
其中,负号是为了确保信息一定是正数或者是0,总不能为负数吧!
(2)为什么底数为2
这是因为,我们只需要信息量满足低概率事件x对应于高的信息量。那么对数的选择是任意的。我们只是遵循信息论的普遍传统,使用2作为对数的底!
信息熵
信息量度量的是一个具体事件发生了所带来的信息,而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值,即所有可能发生事件所带来的信息量的期望。即
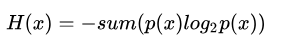
转换一下: