python machine learning

函数缺陷定位 Function Defect Location

Posted by Zreal on November 8, 2018

函数缺陷定位

利用神经网络算法计算函数嫌疑度

思路：

输入：n维向量Vec_i,代表在样例i中，n个函数，各自出现的次数。Vec_i[j]代表第j个函数在第i个样例中出现的次数

输出：0或1，1代表该输入的该样例为错误样例，0代表输入样例为正确样例

训练：totalinfo训练集，每个version训练一个神经网络。

测试：构造测试集，例如计算第i个函数的嫌疑度，另Vec_test[i]=1，其他置0；

步骤：

（所需头文件）

1
2
3
4
5
6
7
8
9
10
11
12

import numpy as np
import pandas as pd
import re
import os
from math import isnan
import torch
import torch.utils.data as data
from torch.utils.data import DataLoader
from torch import nn,optim
from torch.autograd import Variable
from sklearn import preprocessing
import matplotlib.pyplot as plt
1.数据读入：

读入正确样本的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

correctdir=os.listdir('outputs/correct/')
function_list=['lgamma','gser','gcf','qgamma','qchisq','infotbl']
#correct_df 储存正确版本下各个样例的函数出现次数的矩阵，DateFrame格式
correct_df=pd.DataFrame(0,columns=function_list,index=correctdir)
#correct_content 储存正确版本下每个样例对应的文件输出内容，字典格式
correct_content={}
for ex in correctdir:
    filepath='outputs/correct/'+ex
    with open(filepath) as f:
        content=f.read()
        correct_content[ex]=content
        f.seek(0,os.SEEK_SET)
        lines=f.readlines()
        for line in lines:
            line=line.strip()        
            if line in function_list:
                correct_df.loc[ex,line]+=1

最后读入数据的样本格式：

correct_df:

img

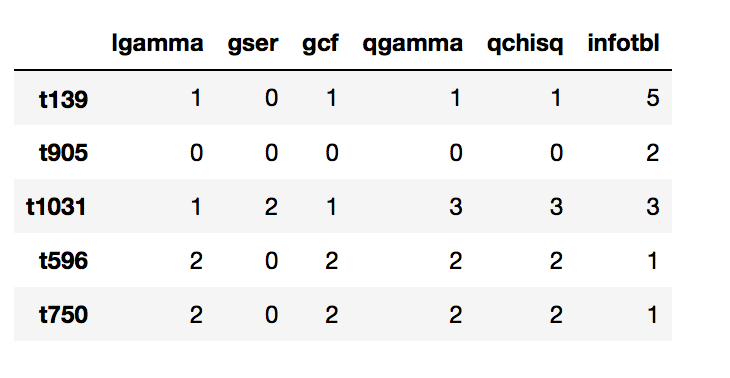
Correct_content:

img

构造对于每个版本进行处理的函数find_num_matrix:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

l=['lgamma','gser','gcf','qgamma','qchisq','infotbl','result']
def find_num_matrix(version,func_list):
    path='outputs/'+version
    example_list=os.listdir(path);
    df=pd.DataFrame(0,columns=l,index=example_list)
    for ex in example_list:
        filepath=path+'/'+ex;
        with open(filepath) as f:
            content=f.read()
            f.seek(0,os.SEEK_SET)
            lines=f.readlines()
            for line in lines:
                line=line.strip()
                if line in function_list:
                    df.loc[ex,line]+=1
            #判断样例是否正确 
            df.loc[ex,'result']=0 if content==correct_content[ex] else 1
    return df

以版本v11为样例，读入数据：

1
2

df=find_num_matrix('v11',function_list)
df.head()

img

对其数据进行一次统计分析：

1

df.apply(pd.value_counts)

img

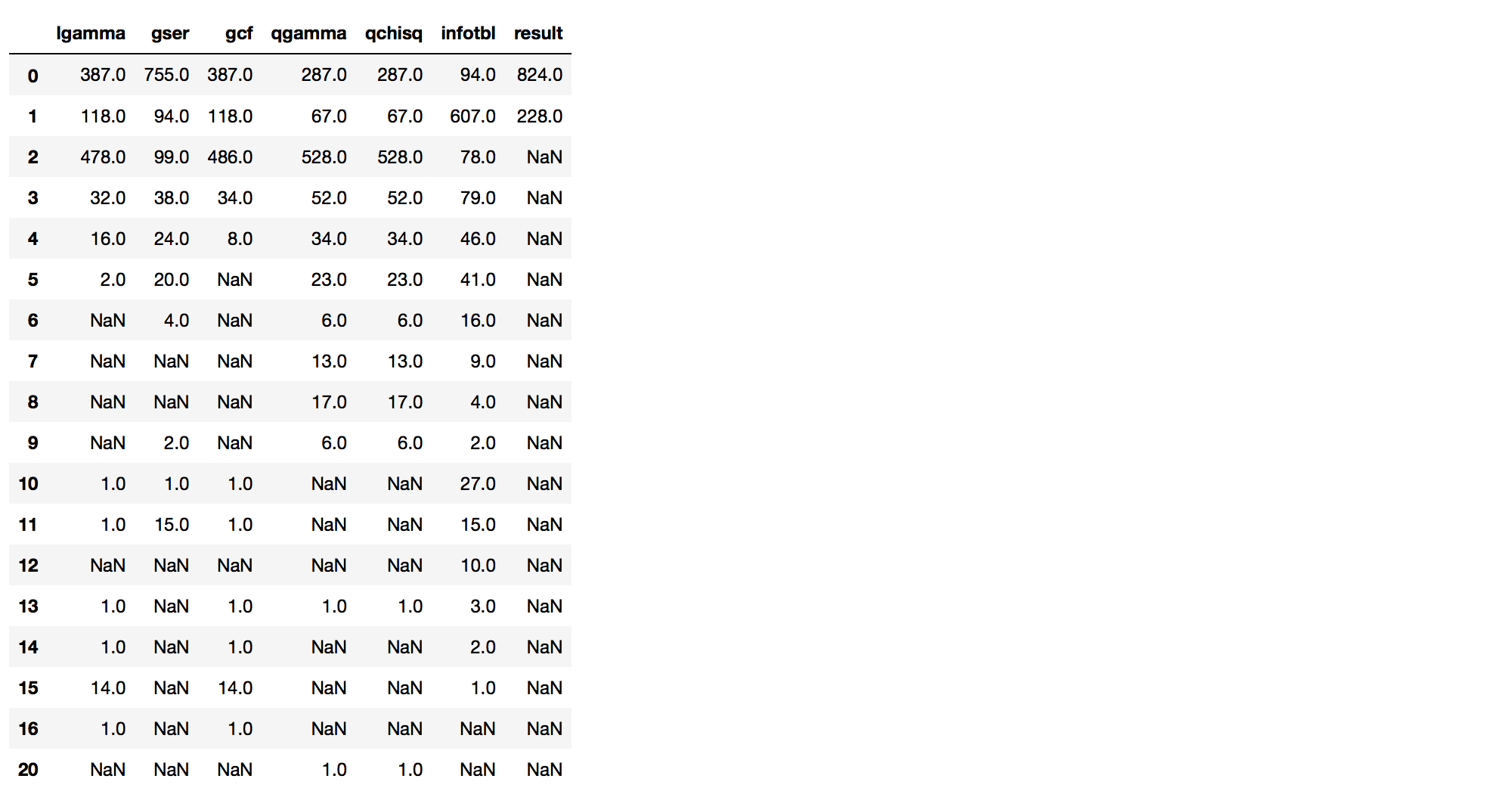
可以看到其正确样例和错误样例的比例并不平均，函数出现的次数集中在0-5之间，但是还是有很多数据的离散度很大。

2.构建网络：

网络结构：

输入层：6个神经元

两个隐藏层：分别拥有6个和4个神经元

输出层：1个神经元

网络层级之间加入激活函数，实现全连接

img

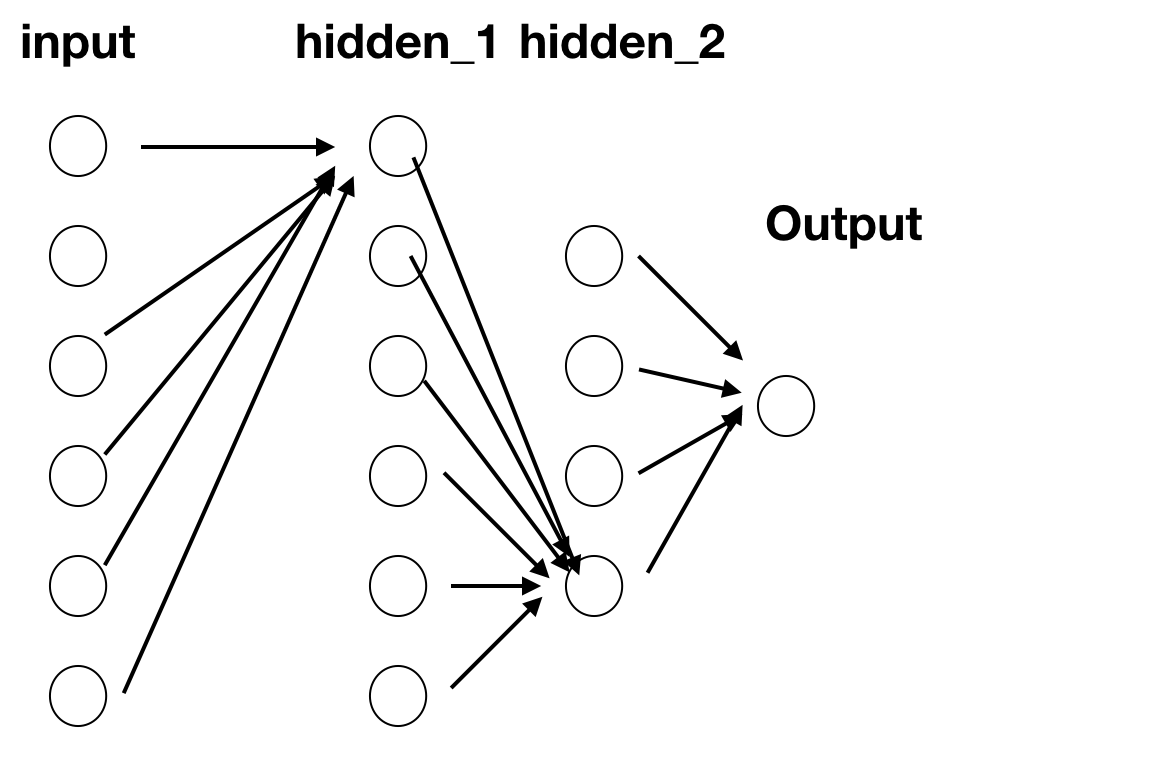
代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13

class Net(nn.Module):
    def __init__(self,in_dim,hidden_n1,hidden_n2,out_dim):
        super(Net,self).__init__()
        self.layer1=nn.Sequential(nn.Linear(in_dim,hidden_n1),nn.ReLU(True))
        self.layer2=nn.Sequential(nn.Linear(hidden_n1,hidden_n2),nn.ReLU(True))
        self.layer3=nn.Sequential(nn.Linear(hidden_n2,out_dim),nn.Sigmoid())
    def forward(self,x):
        x=self.layer1(x)
        x=self.layer2(x)
        x=self.layer3(x)
        return x
#定义网络结构
model=Net(6,6,4,1)

构建输入数据的数据加载嫌疑du容器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#自定义数据集加载容器
class MyDataset(data.Dataset):
    def __init__(self,X,Y):
            self.X=X
            self.Y=Y
    def __getitem__(self,index):
        x,y=self.X[index],self.Y[index]
        return x,y
    def __len__(self):
        return len(self.X)    
#自定义归一化函数
def MinMaxScaler(a):
    for i in range(len(a)):
        s=sum(a[i]);
        a[i]=a[i]/s if s!=0 else 0
    return a
#构建数据集
df_X=df[function_list]
df_Y=df['result']
Xx=MinMaxScaler(X)
Y=np.expand_dims(Y,axis=1)
t_X=torch.FloatTensor(Xx)
t_Y=torch.FloatTensor(Y)
dataset=MyDataset(t_X,t_Y)
batch_size=8
loader=DataLoader(dataset,batch_size=batch_size,shuffle=True)
3.网络训练及测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

learning_rate=0.001
criterion=nn.MSELoss()
optimizer=optim.Adam(model.parameters(),lr=learning_rate)
model.train()
eval_loss=0
epoch=10
loss_list=[]
for i in range(epoch):
    for j,data in enumerate(loader):
        train_x,train_y=data
        train_x=train_x.view(train_x.size(0),-1)
        train_x=Variable(train_x)
        train_y=Variable(train_y)
        out=model(train_x)
        loss=criterion(out,train_y)
        loss.backward()
        optimizer.step()
        if (j+1)%4==0:
            loss_list.append(loss)
            print("epoch:{}      num:{}      loss:{}\n".format(i,(j+1)/4,loss))

训练结果

img

将其损失函数的值可视化：

1
2
3
4

fig=plt.figure(figsize=(10,10))
ax=fig.add_subplot(1,1,1)
ax.plot(range(0,len(loss_list)),loss_list,'r-')
plt.show()

img

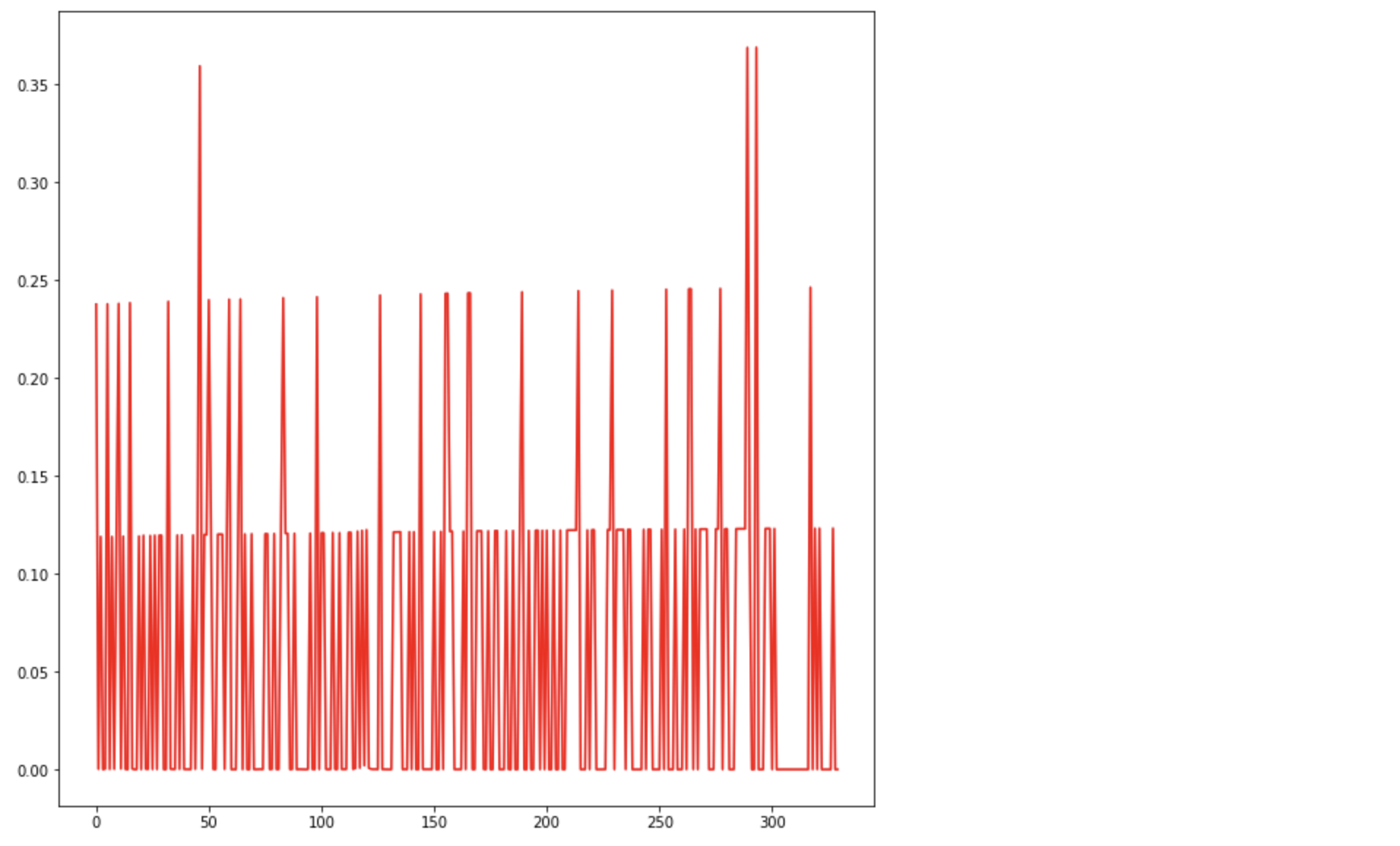
emmmmmm这个损失函数的结果有点感人，可以发现其损失函数一直没有收敛。是不是说明了函数出现的次数与其样例是否错误无太大直接关系

还是用模型测试一下，看一下在版本v11中各个函数的嫌疑度。

1
2
3
4
5
6
7
8
9

testx=np.array([[1,0,0,0,0,0],[0,1,0,0,0,0],[0,0,1,0,0,0],[0,0,0,1,0,0],[0,0,0,0,1,0],
                [0,0,0,0,0,1]],dtype=float)
testy=np.zeros((1,6))
testx=torch.FloatTensor(testx)
testy=torch.FloatTensor(testy)
for i in testx:
    i=Variable(i)
    out=model(i)
    print(out)

img

可以看到结果和预想中的一样糟糕，在之前的比较中v11错误的是gser函数，但是比较模型算出的相对嫌疑度，gser的嫌疑度不是最高的，因此预测失败

结论：

用神经网络的方法探究函数在样例中出现的次数与其嫌疑度之间的关系，其出现次数和其嫌疑度没有直观联系

利用模型融合计算函数嫌疑度

思路
  • 挑选已有的计算嫌疑度的模型
  • 对每一组数据用不同的嫌疑度模型进行嫌疑度计算
  • 设计一套对模型准确度打分的公式
  • 根据已有版本的错误函数的定位，对每一种计算模型进行打分
  • 选取分数最高的模型，进行下一步预测
步骤

（所需头文件）

1
2
3
4
5

import numpy as np
import pandas as pd
import os
import math
import re
1.数据预处理

首先找出之前版本在代码层级上，哪个函数出现了错误，这些数据算是之后模型打分的评判标准

1
2
3
4
5
6
7
8

#错误函数记录在most_suspectfunction的字典中
most_suspectfunction={}
#compare.txt是已经整理好的之前版本代码层级的错误结果
with open('compare.txt') as fc:
    for line in fc.readlines():
        l=line.strip('\n').split(',');
        print
        most_suspectfunction['v'+l[0]]=l[2]

将正确版本的输出内容用字典储存

1
2
3
4
5
6
7

correct_dir=os.listdir('outputs/correct/')
correct_content={}
for ex in correct_dir:
    filepath='outputs/correct/'+ex;
    with open(filepath) as f:
        content=f.read();
        correct_content[ex]=content

对于每个版本的具体数据进行记录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

function_list=['lgamma','gser','gcf','qgamma','qchisq','infotbl']
#Ncf 包含该函数的错误样例的个数
#Nuf 不包含该函数的错误样例的个数
#Ncs 包含该函数的正确阳历的个数
#Nus 不包含该函数的正确样例的个数
#Nc 包含该函数的样例的个数
#Nu 不包含该函数的样例的个数
#Ns 正确样例的个数
#Nf 错误样例的个数

def find_data_of_version(version,function_list):
    df_column=['Ncf','Nuf','Ncs','Nus','Nc','Nu','Ns','Nf']
    pc=0
    fc=0
    df=pd.DataFrame(0,index=function_list,columns=df_column)
    path='outputs/'+version
    example_list=os.listdir(path);
    for ex in example_list:
        filepath=path+'/'+ex
        with open(filepath) as f:
            content=f.read()
            #如果该样例正确
            if correct_content[ex]==content:
                pc+=1
                for func in function_list:
                    if content.find(func)!=-1:
                        df.loc[func,'Ncs']+=1
                        df.loc[func,'Nc']+=1
                    else:
                        df.loc[func,'Nus']+=1
                        df.loc[func,'Nu']+=1
                        
            else:
                fc+=1
                for func in function_list:
                    if content.find(func)!=-1:
                        df.loc[func,'Ncf']+=1
                        df.loc[func,'Nc']+=1
                    else:
                        df.loc[func,'Nuf']+=1
                        df.loc[func,'Nu']+=1
                        
    df['Ns']=pc
    df['Nf']=fc
    return df

生成的df 为一个DataFrame的矩阵，以v11为例：

img

2.计算嫌疑度：

我们选取了四个模型来进行比较，分别是

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#Tarantula
def Tarantula(series):
    if series['Ncf']==0:
        return 0
    else:
        value=(series['Ncf']/series['Nf'])/((series['Ncf']/series['Nf'])+(series['Ncs']/series['Ns']))
        return value
#Kulczynski
def Kulczynski(series):
    if (series['Nuf']+series['Ncs'])==0:
        return 0
    else:
        value=series['Ncf']/(series['Nuf']+series['Ncs'])
        return value
#Ochiai 
def Ochiai(series):
    if series['Nf']==0 or (series['Ncf']+series['Ncs'])==0:
        return 0
    else:
        value=series['Ncf']/math.sqrt(series['Nf']*(series['Ncf']+series['Ncs']))
        return value
#Zoltar
def Zoltar(series):
    if (series['Ncf']+series['Nuf']+series['Ncs']+series['Nuf']*series['Ncs']*10000/series['Ncf'])==0:
        return 0
    else:
        value=series['Ncf']/(series['Ncf']+series['Nuf']+series['Ncs']+series['Nuf']*series['Ncs']*10000/series['Ncf'])
        return value

计算嫌疑度：

1
2
3
4
5
6
7
8
9

def cal_info(version_list,function_list,cal_method):
    df=pd.DataFrame(index=version_list,columns=function_list)
    for version in version_list:
        df_data=find_data_of_version(version,function_list)
        for func in function_list:
            Series=df_data.loc[func]
            value=cal_method(Series)
            df.loc[version,func]=value
    return df

计算结果如下，以Tarantula

1
2

data=cal_info(version_list,function_list,Tarantula)
print(data)

img

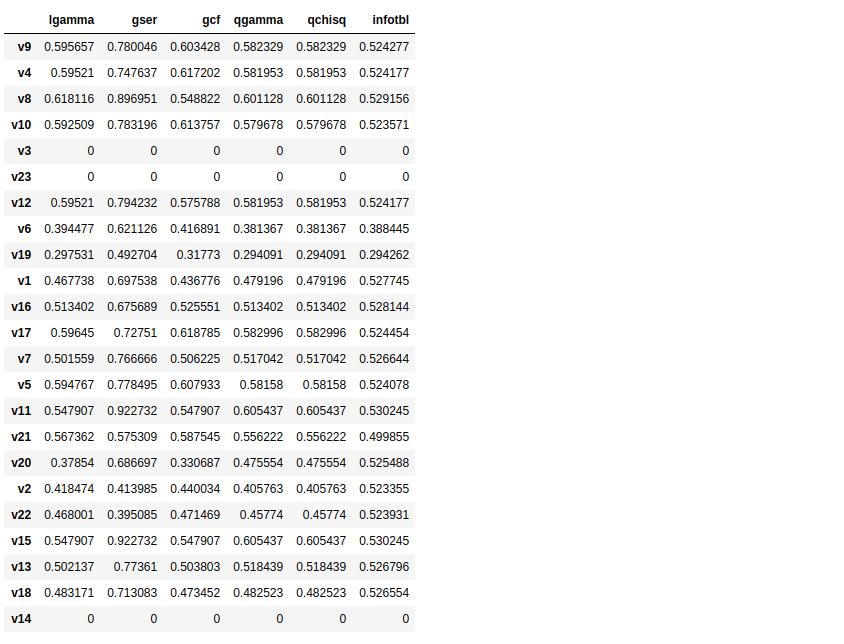
3.构建打分系统：

首先定义一个概念为相对嫌疑度，为在该版本中，某函数相对其他所有函数的嫌疑度

这样只比较函数嫌疑度之间的相对大小: 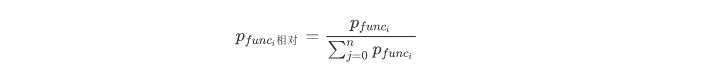img 如果该函数为错误函数，应该给予模型一定奖励： img

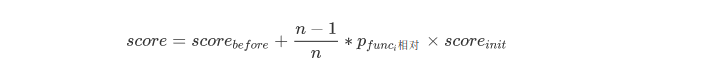
如果该函数不为错误函数，则应该给予模型一定惩罚

img

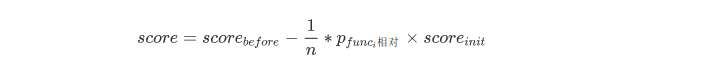
我们以10分为初始分数

最后将所有的版本取求和取平均可得到最终模型得分

附：

如果版本附带时间信息，我们应该对于不同的版本给予不同的权值，例如新的版本在分数中的权值占比应该更大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def give_score(data,most_suspectfunction):
    sub_score=[]
    for ver in data.index:
        error_func=most_suspectfunction[ver]
        sc=10
        sum_proportion=sum(data.loc[ver])
        if sum_proportion==0:
            continue
        for func in data.columns:
            if func==error_func:
                sc+=data.loc[ver,func]/sum_proportion*(len(data.loc[ver])-1)/len(data.loc[ver])*10
            else:
                sc-=data.loc[ver,func]/sum_proportion/len(data.loc[ver])*10
        sub_score.append(sc)
    score=sum(sub_score)/len(sub_score)
    return score
4.对所有模型进行打分
1
2
3
4
5
6
7
8
9
10
11
12

cal_method_name_list=['Tarantula','Kulczynski','Ochiai','Zoltar']
cal_method_dic={'Tarantula':Tarantula,'Kulczynski':Kulczynski,'Ochiai':Ochiai,'Zoltar':Zoltar}
def choose_the_best_model(cal_method_name_list,cal_method_dic,version_list,function_list):
    scoremap={}
    for way in cal_method_name_list:
        data=cal_info(version_list,function_list,cal_method_dic[way])
        score=give_score(data,most_suspectfunction)
        scoremap[way]=score;
    return scoremap

results=choose_the_best_model(cal_method_name_list,cal_method_dic,version_list,function_list)
print(results)

img

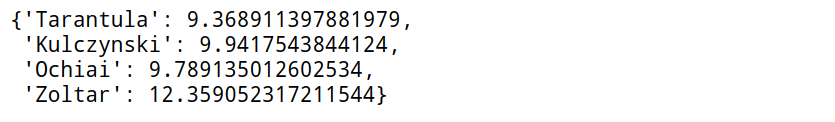
可以看到分数最高的是Zoltar函数

下面用Zoltar函数来进行函数嫌疑度的计算

1
2

data_Zoltar=cal_info(version_list,function_list,Zoltar)
print(data_Zoltar)

img

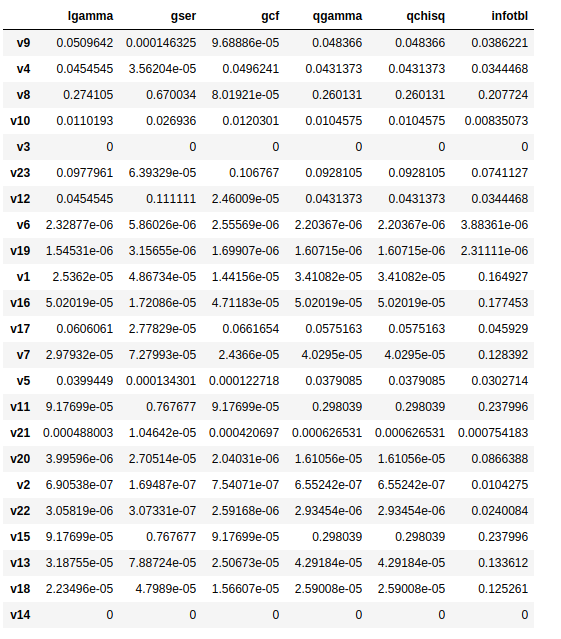
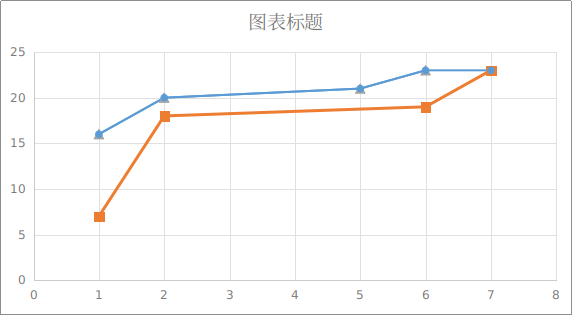
将每个版本中每个函数的嫌疑度计算出来后，我们对其进行Topn作图：

img

我们做了两条折线进行对比，其中蓝色的线为用Zoltar公式计算嫌疑度，橙色的线为用Tarantula公式计算的嫌疑度，可以看到蓝色的线，整体在黄色的线的上方。故Zoltar公式在这些版本中的预测效果要远高于Tarantula，因此也侧面证明了打分公式的正确性。

CATALOG
    FEATURED TAGS
    python TOEFL Reading C++ TOEFL Writing OS Design Pattern ML Hadoop JAVA Machine Learning Math
    FRIENDS